Non-alphanumeric C code - a lab notebook
Introduction⌗
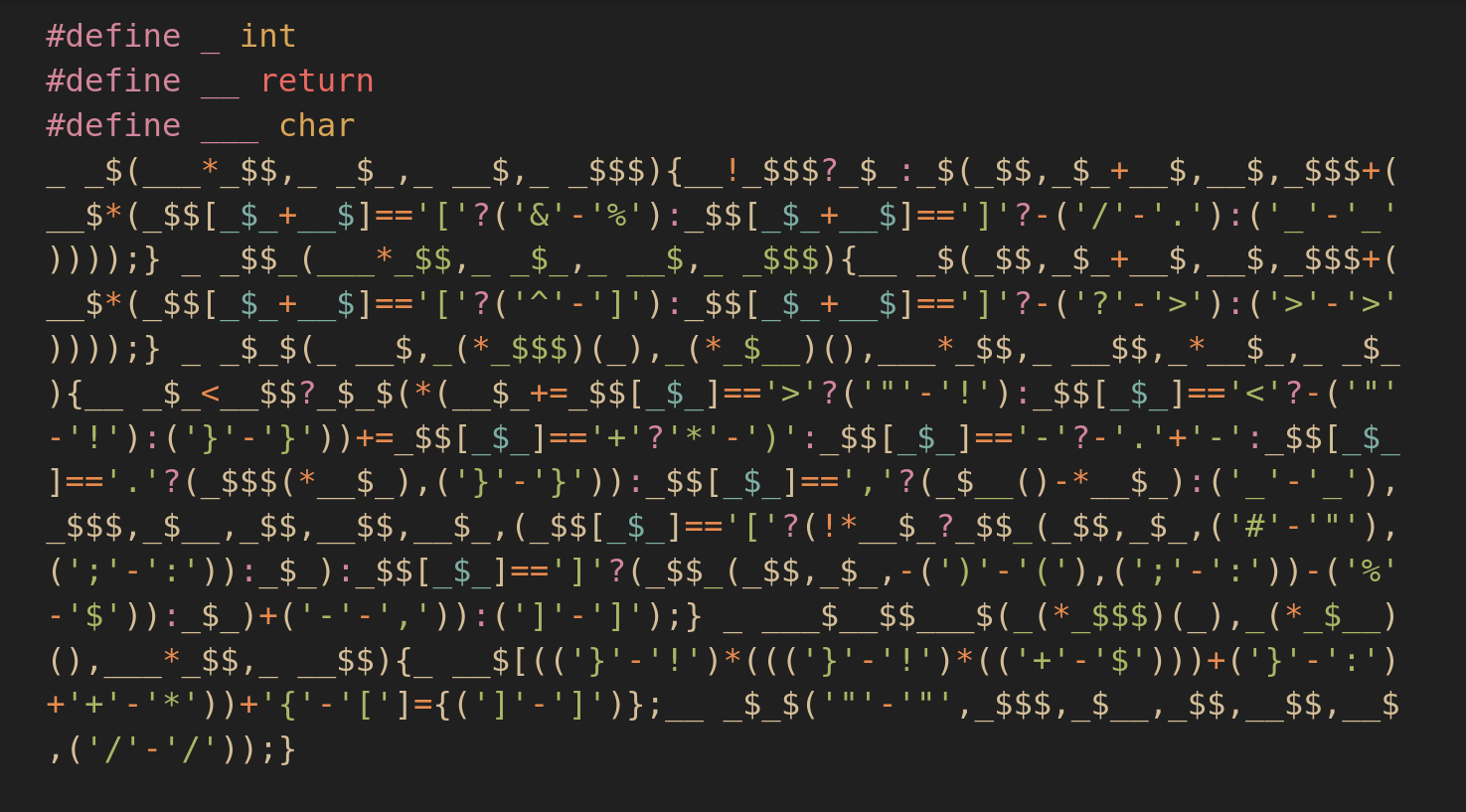
In January of 2021, one of my Discord servers was visited by a person who demonstrated a non-alphanumeric snippet of code written in C.
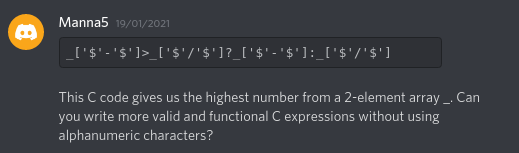
Just being myself, initially I wanted to see if the non-alphanumeric subset of C is Turing-complete. The simplest Turing-complete device I could think of around that time was the Minsky machine, for which I made my own notation.
– A relatively efficient fibonacci function in non-alphanumeric C.
Minsky Machine is, simply put, a computer capable of storing two infinitely large numbers in its memory. It can perform two operations - inc X (increment X-th number) and dec X, Y (decrement X-th number if it’s greater than zero, otherwise jump to instruction Y).
This example Minsky machine program loops infinitely:
A Minsky machine program in my notation is a list of integer tuples. Thinking in terms of a single tuple (numbers x and y), which is equivalent to a single instruction:
- If the
yis equal to -1, then this instruction increments the register given byx. - If the
yis not equal to -1, then this instruction decrements the register given byxif it’s greater than zero. Otherwise, the instruction pointer is altered to point the instruction given byy.
It’s possible to express this program in terms of C code:
As an inquiring mind, you might be wondering how is this extremely simple set of instructions Turing-complete. The answer to this question is given by the textbook “The Theory of Parsing, Translation, and Compiling” from 1972, but to keep things simple, I won’t provide a proof right now.
Either way, having linked Minsky machines, turing completeness and non-alphanumeric C code in my head, I sketched up the following program:
Passing it through the C preprocessor yields exactly what I was looking for:
% gcc -E c1.c | perl -pe "s/^#.*\n$//g;"
__='$'-'$',___,____;_(){((__==(('%'-'$')))?(___++
):(((__==((('%'-'$')+('%'-'$'))))?(___--):(__))))
;__++;_();}
I define a bunch of numeric constants obtained by questionably smart arithmetical manipulation, two counters and construct a program that increments C1, decrements C1 and loops infinitely - but it’s a start. Having written this, I felt that translating Minsky machines to non-alphanumeric C might be trivial. In fact, all that needs to be done is the jumping behavior of decrementation, which can be accomplished by reassigning the instruction pointer, and the infinite looping problem can be solved by checking if the instruction pointer didn’t go out of bounds of the program. Having figured that all out and written a Perl script that automates the translation to some degree, I was happy that I played with this odd concept for a while and forgot about it for good. After all - I had something better to do back then.
The fun part⌗
I wrote a transpiler that targets non-alphanumeric C, which I explain further into the post - it contains a lot of technical terms, assumes knowledge of mathematics, APL, and nifty C tricks. For now though, let’s play with this little black box.
I start with a barebones fibonacci function:
First, I turn the entire function into a single expression for convenience:
Then, I remove all the whitespace and replace the names with their uppercase counterparts (so they’re picked up by the transpiler).
I can abuse the implicit int rule to get rid of the type declarations, but I have to force the compiler to emit a #define directive for return:
And after invoking our compiler, I get the following magical nonsense:
There are a few obvious improvements that I could make ( and the precedence-founded parenthesis dropping):
Isn’t it beautiful? And it works too! But… what about my initial goal? I still don’t have a concrete proof of Turing completeness and going the simple Minsky Machine route doesn’t sound excessively fun. Let’s implement Brainfuck in our C subset instead! I sketched the following, normal Brainfuck interpreter in C:
It’s fairly self-explanatory, so I’ll avoid getting into details. What’s more interesting is how to turn our code into the crazy, amazing, non-alphanumeric form.
I started off by turning a bunch of local variables to parameters and replacing some if statements. Then, I split the match function to avoid a do..while loop:
From there, match is simple to turn into an expression. I also turned match_loop into a recursive function that doesn’t make use of the while construct. I rolled up the if statement in match_loop, and in the meantime, I transformed runbf using the same logic, getting rid of the for loop:
Now, I made runbf_2 recursive and collapsed if statements into ternaries.
Nearly done! I added a dummy parameter to runbf_2 and relied on the evaluation order to set the *tape value, while casually calling runbf_2. The last step is collapsing the final if statement into a ternary.
Finally, I renamed all the symbols and prepared the source code for compilation. I didn’t manage to get rid of return, char and int, so I defined these:
After passing it through the compiler, that’s the output I got:
Let’s grab a “Hello World” program in brainfuck and run my majestic non-alphanumeric interpreter on it:
% cat hello.c
#include <stdio.h>
#include "output.c"
int main(void) {
char * code = "++++++++++[>+++++++>++++++++++>+++>+<<<<-]>++.>+.+++++++..+++.>++.<<+++++++++++++++.>.+++.------.--------.>+.>.";
___$__$$___$(putchar, getchar, code, strlen(code));
}
% gcc hello.c -o hello && ./hello
Hello World!
The compiler - constant generation⌗
In October of 2021, the circumstances made me remember the idea I had with obtaining numbers via subtracting ASCII character codes. I had some time on my hands (around 30 minutes) since I wasn’t home at the time, but I had access to a computer, so I thought that I can make a program that turns any number into a non-alphanumeric C expression to kill some time.
First, I asked my APL session to give me all the non-alphanumeric characters (everything in range 33 to 126 that isn’t a lowercase letter, uppercase letter or a digit) that aren’t problematic (aren’t a quote or a slash):
ns.cs←(⎕UCS∘(32∘+)⍳93)~∊⎕A ⎕D(⎕C ⎕A)'''' '\'
Now, since the numbers in their basic form are represented as character minus character ('X'-'Y'), I generated a table of all possible combinations of it using the outer product:
∘.,⍨ns.cs
Then, I tied the resulting character pairs with their ASCII code difference and turned it into a simple list:
,{⍵,⍥⊂¨-/¨⎕UCS¨⍵}∘.,⍨cs
Next up, I removed all the pairs that sum up to a negative number or zero and sorted the results descendingly, starting with the pairs that have the largest difference:
ns.keys←{⌽⍵[⍋2∘⊃¨⍵]}{⍵/⍨{0<2⊃⍵}¨⍵},{⍵,⍥⊂¨-/¨⎕UCS¨⍵}∘.,⍨cs
Finally, for convenience I made a separate vector out of the 2nd values in the vector:
2∘⊃¨ns.keys
None of this data ever changes, so I wrapped it into a setup function that precomputes it:
setup←{
⍝ the cvt namespace with precomputed data for
⍝ the initial character set.
ns←⎕NS ⍬
⍝ non-alphanumeric character set.
ns.cs←(⎕UCS∘(32∘+)⍳93)~∊⎕A ⎕D(⎕C ⎕A)'''' '\'
⍝ --> quote a string.
ns.quot←{'''',⍵,''''}
⍝ sort a vector of tuples based on the second element.
sortk←{⌽⍵[⍋2∘⊃¨⍵]}
⍝ --> vector of tuples of character pairs that yield
⍝ a given result when subtracted as ASCII codepoints.
ns.keys←sortk{⍵/⍨{0≤2⊃⍵}¨⍵},{⍵,⍥⊂¨-/¨⎕UCS¨⍵}∘.,⍨ns.cs
⍝ every second element extracted from the tuples.
ns.ord←2∘⊃¨ns.keys
ns
}
Then, I used the data I just obtained to create a function, which generates pairs of ASCII character differences that sum up to a given number:
convert 162
┌──┬──┬──┐
│}!│}:│^[│
└──┴──┴──┘
⍝ A-ha! ('}'-'!')+('}'-':')+('^'-'[') must be equal to 162.
The basic algorithm is fairly simple:
- Take the the largest element from the
keysvector which is lesser or equal to the number curretly processed. - Push the element’s character tuple to the result list.
- Subtract the element’s ASCII codepoint difference from the input.
- Repeat the process until the number is zero.
An implementation of this algorithm follows:
convert←{
prop←⍺
⍝ Encode a number.
eN←{
⍝ initialise the result vector; if the number to convert
⍝ is zero, return it.
⍺←⍬ ⋄ ⍵=0:⍺
⍝ pick a list of tuples from keys which second element is the
⍝ maximum value smaller or equal to the number to convert.
⍝ pick a random tuple from this list.
x y←(?∘≢⊃⊢) prop.keys/⍨prop.ord=2⊃⊃prop.keys/⍨⍵≥prop.ord
⍝ append the results, subtract from the input
⍝ number and recurse.
(⍺,⊂x)∇ ⍵-y
}
⍵=0:⊂'$$'⋄eN ⍵
}
(?∘≢⊃⊢) picks a random element from a vector, because it’s equivalent to {(?≢⍵)⊃⍵}, which takes a random number in range 1 to the length of vector, and picks the element with the index given by this random number.
The next step is converting the pairs intto actual C code, and noticing a certain issue:
convert 1252
┌──┬──┬──┬──┬──┬──┬──┬──┬──┬──┬──┬──┬──┬──┐
│}!│}!│}!│}!│}!│}!│}!│}!│}!│}!│}!│}!│}!│[#│
└──┴──┴──┴──┴──┴──┴──┴──┴──┴──┴──┴──┴──┴──┘
1252 isn’t that big of a number, yet it yields so many operations. Thankfully, there exists a simple fix for this issue - . It should be said that there exists a threshold for which this transformation has an adventage over the naive method. The algorithm I implemented performs it when .
x←eN 1513
x
┌──┬──┬──┬──┬──┬──┬──┬──┬──┬──┬──┬──┬──┬──┬──┬──┬──┬──┐
│}!│}!│}!│}!│}!│}!│}!│}!│}!│}!│}!│}!│}!│}!│}!│}!│`:│,)│
└──┴──┴──┴──┴──┴──┴──┴──┴──┴──┴──┴──┴──┴──┴──┴──┴──┴──┘
After obtaining the naive transformation result, I grouped the additions using my favourite APL operator:
↓,∘≢⌸x
┌───────┬──────┬──────┐
│┌──┬──┐│┌──┬─┐│┌──┬─┐│
││}!│16│││`:│1│││,)│1││
│└──┴──┘│└──┴─┘│└──┴─┘│
└───────┴──────┴──────┘
The full code follows:
cp←(⊣,'+',⊢)/
cvts←{'(',(prop.quot ⍺),'-',(prop.quot ⍵),')'}/
cvte←{
emit←{
5≤2⊃⍵:'(',(cvts⊃⍵),'*(',(cvte 2⊃⍵),'))'
x y←⍵ ⋄ cp↑y⍴⊂cvts x
}
⍵≠0:∊cp emit¨↓,∘≢⌸eN ⍵
⊃cvts 2⍴rE prop.cs
}
After wrapping everything in a function, I managed to confirm that the code emits reasonable output:
cvtp cvt 12523
(('}'-'!')*(('}'-'!')+('['-'/')))+('/'-'$')
% cat code.c
#include <stdio.h>
int main(void) {
printf("%d", (('}'-'!')*(('}'-'!')+('['-'/')))+('/'-'$'));
}
% ./code
12523
Around then, my time ran out, but when I was home, approached the entire problem from a different standpoint. To create a Turing-complete language, I to storing data one way or another. In C, which is the language I target, the most reasonable choice is using variables. Either way, variables and functions require an accompanying identifier, and underscore-only names would be incredibly long. Thankfully, GNU C allows putting the dollar sign in identifiers, so I can employ some sort of binary counting in the identifier names:
6.42 Dollar Signs in Identifier Names
In GNU C, you may normally use dollar signs in identifier names. This is because many traditional C implementations allow such identifiers. However, dollar signs in identifiers are not supported on a few target machines, typically because the target assembler does not allow them.
This doesn’t apply to preprocessor macros though, so all-underscore names will be reserved by the compiler for use as macros.
If all the defined names are stored as a vector in a variable x, assuming $ as 0 and _ as 1, one can generate identifiers by treating their indices as binary numbers:
{'$_'[1+2⊥⍣¯1⊢⍵]}¨⍳≢x
┌─┬──┬──┬───┬───┬───┐
│_│_$│__│_$$│_$_│__$│
└─┴──┴──┴───┴───┴───┘
…but the underscores are still here, and that’s not what I wanted. Let’s remove these then:
{⍵/⍨1≠≢∘∪¨⍵}{'$_'[1+2⊥⍣¯1⊢⍵]}¨⍳≢x
┌──┬───┬───┬───┐
│_$│_$$│_$_│__$│
└──┴───┴───┴───┘
The problem with this solution alone is fairly clear - I wanted 6 identifier names, but after purging the invalid ones I’m left with only four, so the goal is to predict (somehow) how many numbers in form 2^n - 1 are there in range from <1, x>. The number I’m looking for is exactly the amount of digits in x’s binary representation, so I added 1+ceil(log_2(x)) to the input to make sure that the code always generates just enough identifier names. Sometimes it will generate too many, so the final reshape takes care of that:
{⍵⍴{⍵/⍨1≠≢∘∪¨⍵}{'$_'[1+2⊥⍣¯1⊢⍵]}¨⍳{⍵+1+⌈2⍟⍵}⍵}≢x
┌──┬───┬───┬───┬────┬────┐
│_$│_$$│_$_│__$│_$$$│_$$_│
└──┴───┴───┴───┴────┴────┘
The algorithm for generating the macro names is obvious:
'_'⍴¨⍨⍳5
┌─┬──┬───┬────┬─────┐
│_│__│___│____│_____│
└─┴──┴───┴────┴─────┘
Having solved two main problems I faced, I glued both of these solutions together to create a working “compiler”:
transcode←{
cf←cvtp∘cvt
dec←{
0=≢⍵:0 ⋄ 11::'Hexadecimal number too big'⎕SIGNAL 11
16⊥16|1-⍨'0123456789abcdef0123456789ABCDEF'⍳¯1↓⍵
}
ra←{code∘←((↑⍵[2])⎕R(↑⍵[1]))code}
code←('\$[^\$]+\$'⎕R{⍕#⍎1↓¯1↓⍵.Match})⍵
code←('\b[0-9][0-9A-Fa-f]*h\b'⎕R{cf dec ⍵.Match})code
code←('\b[0-9]+\b'⎕R{cf⍎⍵.Match})code
pairs←⍺{⍵ ⍺}¨'_'⍴¨⍨⍳≢⍺
defc←{∊'#define '(⍵[1])' '(⍵[2])}¨pairs
_←ra¨pairs
fr←∪('[A-Z]+'⎕S{⍵.Match})code
ids←{⍵/⍨1≠≢∘∪¨⍵}{'$_'[1+2⊥⍣¯1⊢⍵]}¨⍳(⊢+∘⌈2∘⍟)≢fr
_←ra¨ids{⍺ ⍵}¨fr
defc,⊂code
}
It supports hexadecimal numbers, decimal numbers, providing custom names to define, automatically replaces uppercase names with their non-alpanumerically encoded counterparts and does the same to numeric constants. I can also insert APL code between dollar signs to have it evaluated and put in the code.
But that’s not everything just yet - I’d like to have a C preprocessor here, something that automatically filters out defines, and runs the APL program I just made. A small shell script tied together with a processing Perl script will do:
Last but not least, I wanted to use the C preprocessor for a purpose. Transforming loops manually isn’t too fun, so a few pre-defined macros in a library file the programmer can include won’t hurt:
Now, I can simplify (for some definition of this word) my brainfuck interpreter using these macros:
Finally, I decided to put all of the code on Github - feel free to play with the compiler yourself.