What does GCD have in common with leap years?

This post originates from a programming puzzle i posted on Github in March this year. If you want to solve it, stop reading the article and try to come up with an explanation why the code below doesn’t print anything. Let’s look at code now:

#define ctz __builtin_ctz
#define R return
#define SI static inline
typedef unsigned U;
typedef int I;

SI U f(U u,U v){I s=ctz(u|v);u>>=ctz(u);do
{v>>=ctz(v);if(u>v){v^=u;u^=v;v^=u;}v-=u;}
while(v);R u<<s;}SI U l(U n){R f(0x50,n)>f
(50,n);}

U lame(U n){R((n%4==0)&&(n%100!=0))||(n%400==0);}

#define M1 0x28f5c28
#define M2 -0x3d70a3d7
#define M3 0x40000000
#define M4 -0x70000000
#define M5 0xa3d70b

U magic(U n){if(!(n&3)&&(M1<(n*M2>>2|n*M3)))R 1;
R(n*M2>>4|n*M4)<M5;}

I main() {
    for(I i=1;i<4000;i++)
        if(lame(i)!=l(i)||lame(i)!=magic(i))
            puts("oh no!");
}

Starting with the main function - it iterates on integers from 1 to 4000 and checks if functions lame, l and magic return the same result for each of these integers. Otherwise, it prints a message on stdout. By looking at the behavior of this program, we can deduce that the behavior of these functions is the same in the given domain.

First method⌗

Briefly skipping magic, the lame function, as the name suggests, is a fairly generic and common way of performing a leap year test. If we take the classical leap year algorithm¹, i.e.

if (year is not divisible by 4) then (it is a common year)
else if (year is not divisible by 100) then (it is a leap year)
else if (year is not divisible by 400) then (it is a common year)
else (it is a leap year) 

… we can see a clear correspondence between it and the somewhat compressed, single line formula. Let’s focus on the l function now, making it a bit more readable for a start.

static inline unsigned f(unsigned u, unsigned v) {
    I s = __builtin_ctz(u | v);
    u >>= __builtin_ctz(u);
    do {
        v >>= __builtin_ctz(v);
        if(u > v) {
            v ^= u;
            u ^= v;
            v ^= u;
        }
        v-=u;
    } while(v);
    R u << s;
}

static inline unsigned l(unsigned n) {
    return f(80, n) > f(50, n);
}

If you paid close attention to the blog post title, it’s probably obvious to you what f does. But let’s analyse it nonetheless. Let’s recall a few basic properties of gcd. We know that $gcd(2a, 2b) = 2*gcd(a, b)$ (Axiom 1), which implies that generally speaking, $gcd(2na, 2nb)=2n*gcd(a,b)$. We extract the n value using __builtin_ctz(u | v) - first, we take bitwise OR of both arguments and then count the trailing zeroes in the result’s binary representation. This yields the smaller amount of trailing zeroes in one of the numbers, so we extract the coefficient we will be attempting to compute later.

There’s a small problem with this algorithm that makes it unsuitable for general purpose computation - it’s missing a check for either u or v being zero. But since we know that u is a year $\therefore u > 0$ and $v \in \{ 50, 80 \}$, the check is redundant.

We also know that $gcd(2n, 2m+1) = gcd(n, 2m+1)$ (Axiom 2) and $gcd(a,b) = gcd(b,a)$. u >>= __builtin_ctz(u); shifts out the trailing zeros out of u, which is equivalent to dividing it by the largest power of 2 that evenly divides it (making u odd), and a line later this time in a loop, we shift out the zeros from v, being given the previous axiom. If both of the numbers are odd, we fall back to the Euclidean algorithm - $gcd(a, b) = gcd(b, a − b)$ (Axiom 3). Finally, the last line of algorithm adjusts the result with the coefficient we extracted when using our 1st axiom.

Having explained it all, let’s think why $gcd(80, n) > gcd(50, n)$ works. Taking prime factors of $80$ and $50$:

      ]CALC.factors 80
2 2 2 2 5
      ]CALC.factors 50
2 5 5

We notice that the extra $2$ coefficients double the value of $gcd(80, n)$ for indices divisible by four (first value added for reference). With factors

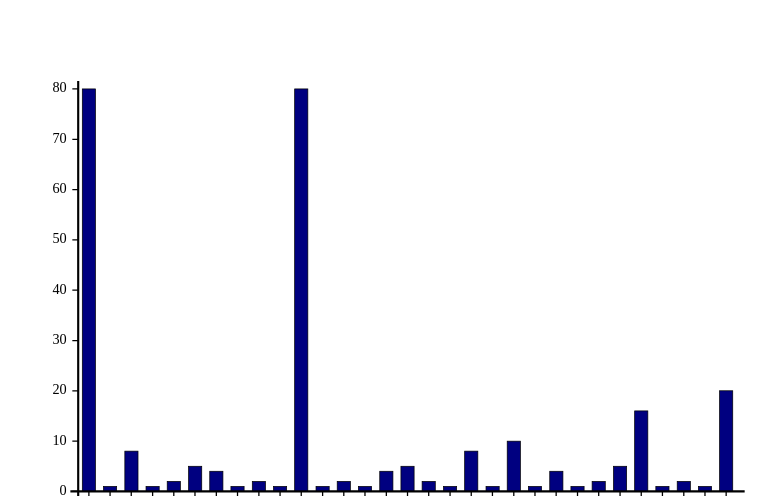
Without factors:

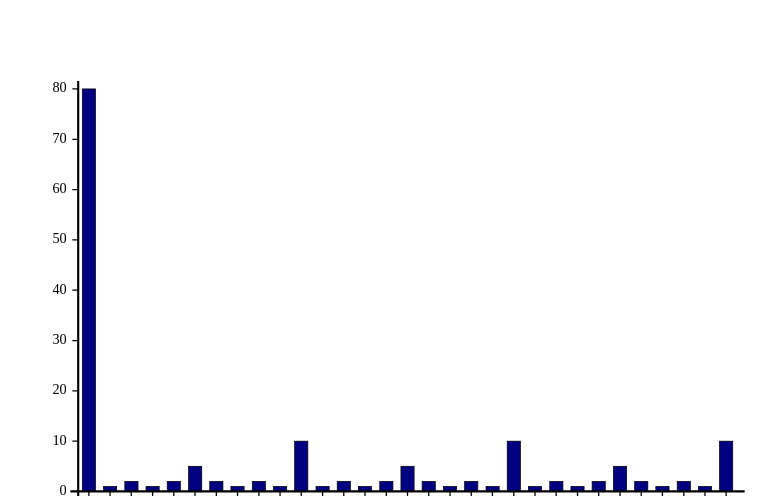
What about the extra 5 coefficient for 50? I’ve observed a small difference on a plot of the same scale as before, but i decided to change the scale, so that the effect is more visible, so we can observe spikes every 100 years:

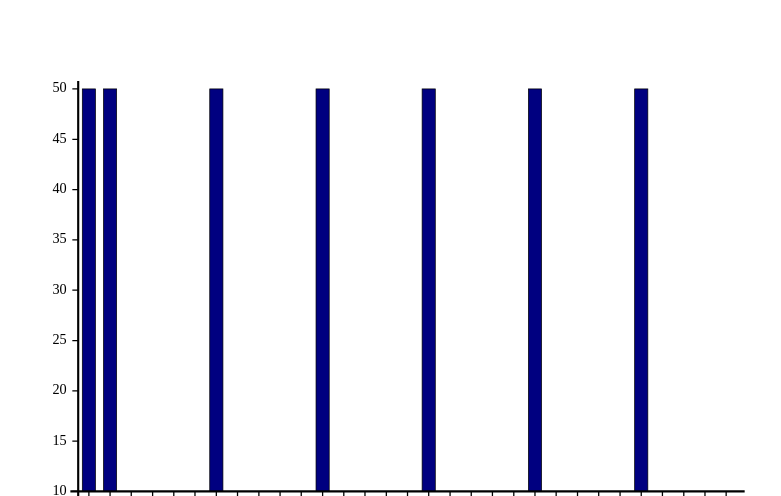
Without the additional 5 factor:

… and of course, for multiplies of $400$, we observe that $lcm(80, 50) = 400$ and knowing that $80 > 50$, the inequality will always hold.

The “magic” method.⌗

First, we observe a clear correspondence between this method and the lame method.

• !(n&3) <=> n%4==0
• M1<(n*M2>>2|n*M3) <=> n%100!=0
• (n*M2>>4|n*M4)<M5 <=> n%400==0

Let’s also recall the magic constants:

#define M1 0x28f5c28
#define M2 -0x3d70a3d7
#define M3 0x40000000
#define M4 -0x70000000
#define M5 0xa3d70b

The correspondence in the first point is obvious, so I’ll skip it (x & 0b11, 4 = 0b100).

The other fragment is a bit more interesting. (n*X>>2|n*M3) (after taking a peek at M3, which coincidentally has the 2nd highest bit set) resembles how C programmers sometimes try to force the compiler into emitting a ror instruction on x86. Simply put, this bit of code multiplies n times a magic constant X and rotates the number right, two bits. Consequently, if we wanted to take n%50!=0, we would rotate one bit, and n%25!=0, which would be equivalent to (M1<<2+3)<n*M2 rotates no bits (we divided by two the left-hand side, we multiply by two the right-hand side, then adjust for the off-by-one in fast modulus). Let’s plug a bunch of numbers into our initial formula.

46*C28F5C29>>2|46*40000000 > 28F5C28
33333336*28F5C28 > 0
8CCCCCCD > 28F5C28
------------
50*C28F5C29>>2|50*40000000 > 28F5C28
CCCCCCD0*28F5C28 > 0
33333334 > 28F5C28
------------
5A*C28F5C29>>2|5A*40000000 > 28F5C28
6666666A*28F5C28 > 0
9999999A > 28F5C28
------------
64*C28F5C29>>2|64*40000000 > 28F5C28
4*28F5C28 > 0
1 > 28F5C28
------------
6E*C28F5C29>>2|6E*40000000 > 28F5C28
9999999E*28F5C28 > 0
A6666667 > 28F5C28
------------
78*C28F5C29>>2|78*40000000 > 28F5C28
33333338*28F5C28 > 0
CCCCCCE > 28F5C28

When we look at the hexadecimal numbers by the left, a fairly obvious conclusion arises - n*M2>>2|n*M3 is small once it hits a certain point in the addition cycle, which so happens to be when 100 is passed as an argument (value is 1). The process of picking the magic numbers so that it’s possible to turn division by a constant into multiplication in modular arithmetic is called modular multiplicative inverse.

The division by 400 algorithm works analogically to the one presented.