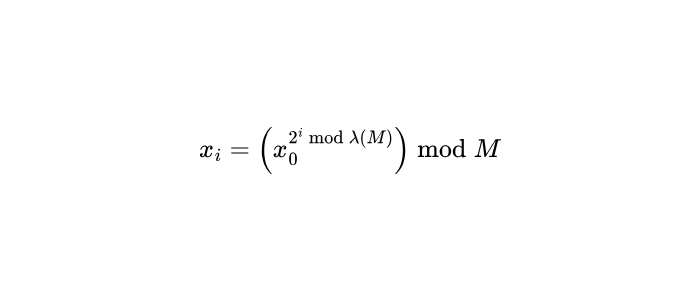
Introduction.⌗

Blum-Blum-Shub (henceforth referred to as BBS) is a pseudorandom number generator uniquely based on the difficulty of factoring large composite numbers. It was introduced by Lenore Blum, Manuel Blum, and Michael Shub in 1986. It is notable for its so-called provable security under certain assumptions, luring many cryptographers to study it.

Let $M = pq$ where $p$ and $q$ are two distinct large primes. The internal state step function is given by:

$x_{n+1} = x_n^2 \mod M$

With $x_0$ being a random seed coprime to $M$ and greater than one. The following requirements are placed on $p$ and $q$ :

They should be Sophie Germain primes, i.e. both $2p + 1$ and $2q + 1$ are also prime.
They should be congruent to 3 modulo 4, i.e. $p \equiv 3 \mod 4$ and $q \equiv 3 \mod 4$ .
$\gcd((p-3)/2, (q-3)/2)$ should be as small as possible, ideally 1.

The random bits are extracted from the internal state at each step. The amount of bits extracted provides a trade-off between speed and security. The most common extraction method is to take the least significant bit of the internal state, but more bits can be extracted at once.

Quadratic residues.⌗

We will start with some preliminary definitions and theorems concerning number-theoretic basis of BBS.

Definition 1. An integer $x \in \mathbb{Z}_n^*$ is called a quadratic residue modulo $n$ if there exists some $y$ such that $y^2 \bmod n = x$ .

Definition 2. The Jacobi symbol $\left( \frac{a}{n} \right)$ is defined as follows: $\left( \frac{a}{n} \right) = \begin{cases} 1 & \text{if } a \text{ is a quadratic residue modulo } n \text{ and } a \not\equiv 0 \mod n, \\ -1 & \text{if } a \text{ is not a quadratic residue modulo } n, \\ 0 & \text{if } a \equiv 0 \mod n. \end{cases}$

Definition 3. Consider $n = pq$ like in the BBS generator. $\mathbb{Z}_n^*$ is then partitioned into two sets of equal cardinality - $\mathbb{Z}_n^{*,-1}$ and $\mathbb{Z}_n^{*,1}$ where $\mathbb{Z}_n^{*,y} = \{a \in \mathbb{Z}_n^* \mid \left( \frac{a}{n} \right) = y\}$ . Logically, none of the elements in $\mathbb{Z}_n^{*,1}$ are quadratic residues modulo $n$ and exactly half of the elements in $\mathbb{Z}_n^{*,-1}$ are quadratic residues modulo $n$ .

Definition 4. A solution to the quadratic residuosity problem (QRP) decides whether some $x \in \mathbb{Z}_n^{*,1}$ is a quadratic residue modulo $n$ .

Theorem 5. An unproven but considered by researchers highly likely assumption is that any PPT (probabilistic polynomial-time) algorithm that solves the QRP has the probability of success at most $1/2 + \varepsilon$ , where $\varepsilon$ is small and in $O(\log n)$ .

Many known partial solutions to the QRP orbit around prime factorisation of $n$ . In particular, quadratic residuosity is efficient to check for prime $n$ , and a number is a quadratic residue modulo $n$ if it’s a quadratic residue modulo every prime factor of $n$ . The practical implication of this is that the factorisation of $n$ can not be known by an adversary. More generally, finding hard to factor semiprimes is a well-known problem in RSA.

This leads many researchers to believe that QRP and prime factorisation are mostly interchangeable in that efficient factorisation of $n$ implies efficient solution to the QRP. Indeed, the most efficient known algorithm for solving the QRP is based on factorisation, but formally speaking an efficient solution to the QRP does not need to imply efficient factorisation of $n$ .

Digging deeper, there is also no proof of the statement that factorization is hard - albeit millenia of research have not yet come up with an efficient factorization method, so it must not be trivial. Accordingly, the security status of BBS is similar to that of RSA.

Circling back.⌗

Let’s discuss how this connects to BBS.

In the specific case of BBS, we have concrete evidence that the assumption of hardness of QRP can be equivalently replaced by the assumption of hardness of factorisation. This was proven by W. B. Alexi, B. Chor, O. Goldreich, and C. P. Schnorr. RSA/Rabin functions: certain parts are as hard as the whole. in SIAM J. Computing, 17(2):194-209, April 1988.

The reduction in Blum, Blum, Shub (1986) proceeds by demonstrating that, if there is a PPT algorithm that operates backwards on the BBS generator (i.e. after observing some consecutive outputs of the generator, it can predict the output preceding them) with a specific probability, then there is also a PPT algorithm that solves the QRP with the same probability.

The original construction assumes that we extract the lowest order bit of the internal state at each step, but it can be generalized to extract more bits at once. Specifically, U.V. Vazirani and V.V. Vazirani, Efficient And Secure Pseudo-Random Number Generation in 25th Annual Symposium on Foundations of Computer Science, 1984, showed that we can securely extract $\mathcal O(\log \log M)$ bits at each step.

The generator can be seeked around to any position using Carmichael’s function of M, which degenerates to $(p - 1)(q - 1) / gcd(p - 1, q - 1)$ via Euler’s theorem, stating that

$f(i) = f(0)^{\left(2^i \bmod \text{Carmichael}(M)\right)} \bmod M$

A concrete (non-asymptotic) proof of correctness is given by A. Sidorenko and B. Schoenmakers, Concrete Security of the Blum-Blum-Shub Pseudorandom Generator. Cryptography and Coding. They claim:

Theorem. Suppose the BBS pseudorandom generator extracting $j$ bits at a time is not $(T_A, \varepsilon)$ -secure. Then there exists an algorithm $F$ that factors the modulus $N$ in expected time

$T_F \leq 36n (\log_2 n) \delta^{-2} (T_A + 2^{2j + 9} n \delta^{-4})$

where $\delta = (2^j - 1)^{-1} M^{-1} \varepsilon$ .

Moving on to factoring, the most efficient known algorithm is the General Number Field Sieve (GNFS), which has a sub-exponential complexity proportional to:

$R \sim \gamma \exp\left((1.9229 + o(1))(\ln N)^{1/3}(\ln \ln N)^{2/3}\right)$

The authors thus approximate the number of clock cycles required to factor an $n$ -bit integer as:

$L(n) \approx 2.8 \cdot 10^{-3} \cdot \exp\left(1.9229(n \ln 2)^{1/3}(\ln(n \ln 2))^{2/3}\right)$

Under the assumption that no algorithm can factor an $n$ -bit Blum prime in less than $L(n)$ clock cycles, the BBS generator is $(T_A, \varepsilon)$ -secure if:

$T_A \leq \frac{L(n)}{36n (\log_2 n) \delta^{-2}} - 2^{2j + 9} n \delta^{-4}$

where $\delta = (2^j - 1)^{-1} M^{-1} \varepsilon$ .

The paper demonstrates a practical application of this result: If we take $M = 2^{20}$ outputs, bound $T_A$ to $2^{100}$ clock cycles and $\varepsilon = 1/2$ . Then, the recommended amount of bits of security is $n = 6800$ , while the amount of bits extracted at each step is $j = 5$ .

Another result is given by S. Chatterjee, A. Menezes, and P. Sarkar Another Look at Tightness, where they demonstrate that some common exceedingly-liberal choices of $n$ and $j$ (in that case $n=768$ and $j=9$ ) lead to lack of tangible security and dismantle the proof. This is however due to the fact that $j$ is way too large, and the double-log bound for $n=768$ is at most $j=2$ or $j=3$ .

Security implications.⌗

It is generally assumed that $p$ and $q$ (and thus $M$ ) remain secret. Further, it is assumed that $x_0$ is secret and similar in magnitude to $M$ .

If $p$ and $q$ become public, we can create a seekable generator per the formula from the introductory section, as the Carmichael function of $M$ can now be feasibly computed. Further, we can approximate the period of the generator and produce a suitable distinguisher.

On the other hand, retaining $p$ and $q$ offers a performance improvement on the side of a legitimate generator. In this case, we observe that finding roots modulo $M$ , in general, is difficult. However, if $p$ and $q$ are known, we can compute the roots modulo $p$ and $q$ separately, and then combine them using the Chinese Remainder Theorem, resulting in three $n$ -bit multiplications rather than a $2n$ -bit multiplication.

For a concrete exposition of how to do this, consider:

$x_p = x_n \mod p,\quad x_q = x_n \mod q,$ $x_p’ = x_p^2 \mod p,\quad x_q’ = x_q^2 \mod q.$

These squarings are faster because $p$ and $q$ are each roughly half the bit-length of $M$ .

We reconstruct $x_{n+1} \mod M$ using:

$M = pq,\quad M_p = q,\quad M_q = p,$ $y_p = q^{-1} \mod p,\quad y_q = p^{-1} \mod q.$

Then, the CRT gives:

$x_{n+1} = (x_p’ \cdot q \cdot y_p + x_q’ \cdot p \cdot y_q) \mod M.$

Specifically, $y_p$ and $y_q$ can be cached as they are constant for a given $M$ . The computation usually proceeds via the EEA.

Toy experiments.⌗

We can begin by taking the two primes for granted and subsequently computing $n=pq$ .

p_hex = "0x29ed85d1e846071f5cdb3b019487401f082c4ac2316db2916fa1278a7c312555b5206e89b52270fe8d54a4f526ce35d0e1716b250f3d76107b4c9ed8ef2dcc30e927a039a960cca04656df06796554db16a6f9b6957b10355226e7f7ef840ea21c45429347a69acd1ad60037741ba0060735c676ed6b6cc453cd402ae5968760980a06ded7765fa086788b2155f69b1d727d346c6f5c45b7231b59f43ee067b33329df7bf0b87123ee1759b3ea17c6391513e8c9ebd13078fa86c08dcf9fa5974c5ca2c4228590b53f929a941b6371dc9b579b824d90fa37ed7e64e00c862e7abb3891d0decb8da754c1e84af3133bd4d3258ae2e96db19c797a7e8159760f6161f66789962df94f95184dd17a7264d1a99db8556044a9640b9a19605d61a79162bd809dc4613d5aa84ac1a20a9c85e5905749c0aeb9542af00bd6b3569fdaf82894f58462e5cc0b114721ea289e8bc0deca4b806a29e38a7308e634de0a8c7510369de020d4bbaf4a01c4dde79b9f5db585b5689d7b905789ab05b7213cb4d176e04508094c9024da06a05f96f8471287808f729770a105781096db76ba2476f6c5efc06a0a05d98a5a8410f6900e09fd100b23f561eb439b11e824b0a614f642d123525f6bf9cd19ac704b740a20948a3ebd3faf88432e822ffe2ca3bbcfbe7846c335f6dd144296916d98f235bc7882008951fff70b7b32d629ca7344178f"
q_hex = "0x643f44a1505bce191f5135f4ba3913fa597830b90f718683cb3b205f01cc1d02a135483b8859f90750cb3caca37183894ec1115d3a1be44aabd017a6c734d8f8af99fca0e4da780ffed8edc51c6fbe21600bafb263ad70356253405b0b3fc0c81550d33b7011a950c0aa5d42eb964de026c9d2dd230d28e7ac1c60cd51c3de7f34181f686c0ab5d4d5af6cb831908eedc85e97d09bd83fbafa598e96aa378796c559d51a4c2cbf86485c4abca09dda3ca1e0eddd373370ca1218e2dcbce6d7097e517ba822b8559a8ce6a7896721c99ef6978480230c650332c0560a9dbe9d242b28fb0ae9074d9727c4754b4ecf93bd6c8f629c5149a75718810bf18225fda6b2c4b5d3afe282c9fb1f9418d73b85d097674bdab297f0913147d679c89f4f1a543fd0b4f30c396206d8b5cf37bbe29fc99d18796fd4c79109eb579a67171d4538021363472f7cd3a68cb28f29779cb2d1d7fc393ecd60f18330ed638fa8f9ceaa00360a4d7077b4eb90dc00347e7ea912c9f9f7945af57af79ed62214cc4b70d2729b912444f4bcea8f62293191104298de8f4c3cd13a08e9a9341e70ca9cf298d0ef5f635fd604e88d00daa999ca1f1b0de1fbd130b8282d03b942d5d8f8c116494709fe213e8114afac4a3af3e47007c985460e9e406e7e01c90b72948006f5cff0a136e7d10f954d54ebb059b112315b14ef723cf493f0cfbee0f602c66f"
p = int(p_hex.replace("\n", ""), 16)
q = int(q_hex.replace("\n", ""), 16)
n = p * q

Then, we can precompute the CRT constants, which is particularly easy in Python:

q_inv_p = pow(q, -1, p)
p_inv_q = pow(p, -1, q)
seed = 123456789 # Any number co-prime to n.
def bbs_next(state):
  xp, xq = state % p, state % q
  xp2, xq2 = pow(xp, 2, p), pow(xq, 2, q)
  return (xp2 * q * q_inv_p + xq2 * p * p_inv_q) % n
def bbs_next_regular(state):
  return pow(state, 2, n)
x_crt = pow(seed, 2, n)
x_reg = x_crt
bits_crt, bits_reg = [], []
for _ in range(128):
  x_crt = bbs_next(x_crt)
  x_reg = bbs_next_regular(x_reg)
  bits_crt.append(str(x_crt & 1))
  bits_reg.append(str(x_reg & 1))
print("Generated bits (CRT):")
print("".join(bits_crt))
print("Generated bits (regular):")
print("".join(bits_reg))

C implementation.⌗

A fully-featured C implementation of the BBS generator is more involved. In this article we will primarily cover the cbbs-rng implementation produced by the author of this article.

The generator supports OpenMP parallelisation for faster generation of the starting state. Some preliminary feature detection code follows:

// ---------------------------------------------------------------------------
//      General research implementation of the Blum Blum Shub
//      random number generator. Written and released to the public
//      domain by Kamila Szewczyk.
// ---------------------------------------------------------------------------
#include <stdio.h>
#include <stdint.h>
#include <stdlib.h>
#include <string.h>
#include <stdarg.h>
#include <math.h>
#include <errno.h>

#ifdef OPENMP
  #include <omp.h>
#endif

// ---------------------------------------------------------------------------
//      Bit integers and OpenMP detection code.
// ---------------------------------------------------------------------------
// Define s.t. desired log2(pq) --> N_BITS.
// For tangible security set at least N_BITS = 8192.
// For demonstration, set N_BITS = 512.
#define N_BITS 8192

typedef unsigned _BitInt(N_BITS) bbsint;
typedef unsigned _BitInt(N_BITS * 2) bbs2int;

#if N_BITS > 1024
  #ifndef OPENMP
    #error "That won't work."
  #endif
#endif

Most importantly, we use the new C23 feature - _BitInt - to define bit integers of arbitrary size. This allows us to work with large numbers without worrying about overflow or performance penalty as accurred with gmp. The values of $p$ , $q$ and $x_0$ must come from a cryptographically secure source, such as /dev/urandom on Linux or CryptGenRandom on Windows:

// ---------------------------------------------------------------------------
//      Cryptographically secure random number source. Used
//      for seeding the generator. Supports DOS, Windows and *NIX platforms.
// ---------------------------------------------------------------------------
static void eprintf(const char * fmt, ...) {
  va_list args;
  va_start(args, fmt);
  vfprintf(stderr, fmt, args);
  va_end(args);
  exit(1);
}

#ifdef _WIN32
#include <windows.h>
#include <fcntl.h>
#include <io.h>
static HCRYPTPROV hp;
static void init_secrandom(void) {
  CryptAcquireContext(&hp, NULL, NULL, PROV_RSA_FULL, CRYPT_VERIFYCONTEXT);
}
static void secrandom(void * buf, size_t len) {
  CryptGenRandom(hp, len, buf);
}
#elif __unix__
#include <fcntl.h>
#include <unistd.h>
static int fd;
static void init_secrandom(void) {
  fd = open("/dev/urandom", O_RDONLY);
  if (fd < 0)
    eprintf("Could not open `/dev/urandom': %s\n", strerror(errno));
}
static void secrandom(void * buf, size_t len) {
  read(fd, buf, len);
}
#elif __MSDOS__
static FILE * f;
static void init_secrandom(void) {
  f = fopen("/dev/urandom$", "rb");
  if (!f)
    eprintf("Could not open `/dev/urandom$': %s\n", strerror(errno));
}
static void secrandom(void * buf, size_t len) { // Doug Kaufman's NOISE.SYS
  fread(buf, 1, len, f);
}
#endif

For primality testing we use generally use the Miller-Rabin test. However, for the sake of performance, we will perform some rudimentary trial division first to weed out the obvious non-primes. This is however not as simple as it may seem: trial divisions of large numbers are excruciatingly slow.

In the cbbs-rng implementation, we use a common trick in cryptography and data compression called the Barrett Reduction. Long story short, we can replace a division by a multiplication with a shift. For pre-generating the table of small primes, we use the Sieve of Atkin.

// ---------------------------------------------------------------------------
//      Low-level, preliminary primality test (fixed size sieve).
//      Pre-generates primes via the Sieve of Atkin.
//      Assumes that inputs to the algorithm `p' are p <= 2^(N_BITS - 1).
//      and further p mod 4 = 3. Also uses Fermat's little theorem.
// ---------------------------------------------------------------------------
#define NPRIMES 4096
static unsigned primes[NPRIMES];
static bbs2int barrett_cache[NPRIMES];
static void populate_barrett_cache(void) {
  int limit = NPRIMES * log2(NPRIMES) * 1.2;
  if (limit < 2) limit = 2;
  char * p = calloc(limit + 1, 1);
  p[2] = p[3] = 1;
  for (int x = 1; x * x <= limit; x++) {
    for (int y = 1; y * y <= limit; y++) {
      int n = 4 * x * x + y * y;
      if (n <= limit && (n % 12 == 1 || n % 12 == 5)) p[n] = !p[n];
      n = 3 * x * x + y * y;
      if (n <= limit && n % 12 == 7) p[n] = !p[n];
      n = 3 * x * x - y * y;
      if (x > y && n <= limit && n % 12 == 11) p[n] = !p[n];
    }
  }
  for (int r = 5; r * r <= limit; r++)
    if (p[r]) for (int i = r * r; i <= limit; i += r * r) p[i] = 0;
  int count = 0;
  for (int i = 2; i <= limit && count < NPRIMES; i++)
    if (p[i]) primes[count++] = i;
  free(p);
  for (unsigned i = 0; i < NPRIMES; i++)
    barrett_cache[i] = ((bbs2int) -1) / primes[i] + 1;
}
static bbsint modexp_half(bbsint base, bbsint e, bbsint mod) {
  bbsint r = 1;
  while (e) {
    if (e & 1)
      r = r * base % mod;
    base = base * base % mod;
    e >>= 1;
  }
  return r;
}
static int p_low(bbsint n) {
  for (unsigned i = 0; i < NPRIMES; i++)
    if (barrett_cache[i] * n < barrett_cache[i]) return 0;
  return modexp_half(2, n - 1, n) == 1; // Fermat.
}

The Miller-Rabin test is then implemented as follows with a variable amount of iterations:

// ---------------------------------------------------------------------------
//      High-level probabilistic primality test (Miller-Rabin).
//      Assumptions are the same as for the low-level test.
//      Uses binary exponentiation with Barrett reductions for speed.
// ---------------------------------------------------------------------------
static int ilog2(bbsint n) { int l = 0; while (n >>= 1) l++; return l; }
static bbsint csrand(bbsint max, int ilog) {
  for (;;) {
    bbsint r; secrandom(&r, N_BITS / 8);
    if ((r >>= N_BITS - ilog) < max) return r;
  }
}
static int p_high(bbsint n, int iter) {
  int s = 0;  bbsint d = n - 1;
  while ((d & 1) == 0) { d >>= 1; s++; }
  int ilog = ilog2(n - 3);
  for (int i = 0; i < iter; i++) {
    bbsint a = 2 + csrand(n - 3, ilog);
    bbsint x = modexp_half(a, d, n);
    if (x == 1 || x == n - 1)
      continue;
    int c = 0;
    for (int r = 1; r < s; r++) {
      x = x * x % n;
      if (x == n - 1) { c = 1; break; }
    }
    if(!c) return 0;
  }
  return 1;
}

Nominally, the inner loop computing $x := x^2 \mod n$ could also use Barrett reductions for improved performance, but the author observed that it is not particularly beneficial in practice.

All these components build up to the main part of our BBS generator which computes the parameters $p$ and $q$ under the condition that they are Sophie Germain primes and Blum integers.

// ---------------------------------------------------------------------------
//      Prime number generation for the BBS algorithm. Resulting p, q are
//      Sophie Germain-safe primes.
//      Yields correct results in 99.99999999999999999999999999999999997%
//      of the cases (2^-128 error rate due to ROUNDS = 64 in Miller-Rabin).
//      `gcd((p-3)/2, (q-3)/2)' should be small for maximised
//      period length. Not strictly necessary; nmplemented here.
//      Per Bertrand postulate we always find a suitable prime.
//      
//      Optimisation:
//      We know that k = (p - 1)/2 (so p = 2k + 1) is prime. Then
//      2^(p - 1) = 1 (mod p) implies that p is prime as well.
// ---------------------------------------------------------------------------
#ifndef OPENMP
  static void generate_primes(bbsint * p1, bbsint * p2) {
    bbsint p, q, r;  const int ROUNDS = 64;
    do {
      p = csrand((((bbsint) 1) << (N_BITS / 2 - 2)), N_BITS / 2 - 2);
      p |= 0b11; r = 2 * p + 1;
    } while (!p_low(r) || !p_high(r, ROUNDS)
          || modexp_half(2, r - 1, r) != 1);
    do {
      q = csrand((((bbsint) 1) << (N_BITS / 2 - 2)), N_BITS / 2 - 2);
      q |= 0b11; r = 2 * q + 1;
    } while (p == q || !p_low(r) || !p_high(r, ROUNDS)
           || modexp_half(2, r - 1, r) != 1);
    *p1 = 2 * p + 1; *p2 = 2 * q + 1;
  }
#else
  static void generate_primes(bbsint * p1, bbsint * p2) {
    const int ROUNDS = 64;  _Atomic(int) found;
    found = 0;
    #pragma omp parallel for
    for (int i = 0; i < omp_get_num_threads(); i++) {
      bbsint p, r;
      do {
        p = csrand((((bbsint) 1) << (N_BITS / 2 - 2)), N_BITS / 2 - 2);
        p |= 0b11; r = 2 * p + 1;
      } while (!found && (!p_low(r) || !p_high(r, ROUNDS)
            || modexp_half(2, r - 1, r) != 1));
      #pragma omp critical
      { if (!found) *p1 = 2 * p + 1, found = 1; }
    }
    found = 0;
    #pragma omp parallel for
    for (int i = 0; i < omp_get_num_threads(); i++) {
      bbsint q, p = *p1, r;
      do {
        q = csrand((((bbsint) 1) << (N_BITS / 2 - 2)) - N_BITS, N_BITS / 2 - 2);
        q |= 0b11; r = 2 * q + 1;
      } while (!found && (!p_low(r) || !p_high(r, ROUNDS)
            || modexp_half(2, r - 1, r) != 1 || 2 * q + 1 == p));
      #pragma omp critical
      { if (!found) *p2 = 2 * q + 1, found = 1; }
    }
  }
#endif

The $\gcd$ function will be necessary to compute the period of the generator. An efficient algorithm for that is given by Stein and implemented below:

// ---------------------------------------------------------------------------
//      Greatest common divisor via Stein's algorithm.
// ---------------------------------------------------------------------------
int ctz(bbsint n) {
  int c = 0; while ((n & 1) == 0 && n != 0) { n >>= 1; c++; } return c;
}
bbsint gcd(bbsint a, bbsint b) {
  if (!a) return b; if (!b) return a;
  int az = ctz(a), bz = ctz(b);
  int shift = az < bz ? az : bz;
  b >>= bz;
  while (a != 0) {
    a >>= az;
    bbsint diff = b - a;
    az = ctz(diff);
    b = a < b ? a : b;
    a = diff & ((bbsint) 1 << (N_BITS - 1)) ? 1 + ~diff : diff;
    if (a == b) return a;
  }
  return b << shift;
}

Finally, the state of the BBS generator itself is represented, initialised and seeked as follows:

// ---------------------------------------------------------------------------
//      Interface to the Blum Blum Shub generator.
// ---------------------------------------------------------------------------
typedef struct { bbsint pq, x, x0, c; int pos; } bbs_t;
static void bbs_new(bbs_t * bbs) {
  bbsint p, q;  generate_primes(&p, &q);
  bbs->pq = p * q;
  for (;;) {
    bbs->x = csrand(bbs->pq, ilog2(bbs->pq));
    if (bbs->x <= 1) continue;
    if (bbs->x % p != 0 && bbs->x % q != 0) break;
  }
  bbs->x0 = bbs->x;
  bbs->c = (p - 1) * (q - 1) / gcd(p - 1, q - 1);
  bbs->pos = 0;
}
static void bbs_step(bbs_t * bbs) {
  bbs2int sq = ((bbs2int) bbs->x) * bbs->x;
  bbs->x = sq % bbs->pq;
  bbs->pos++;
}
static bbsint modexp(bbsint base, bbsint e, bbsint mod) {
  bbsint r = 1;
  while (e) {
    if (e & 1)
      r = (((bbs2int) r) * base) % mod;
    base = (((bbs2int) base) * base) % mod;
    e >>= 1;
  }
  return r;
}
static void bbs_set(bbs_t * bbs, unsigned i) {
  bbsint arg = modexp(2, i, bbs->c);
  bbs->x = modexp(bbs->x0, arg, bbs->pq);
  bbs->pos = i;
}

Simply advancing the generator is performed by the following procedures:

static bbsint bbs_next(bbs_t * bbs, int bits) {
  bbsint r = 0;
  for (int i = bits; i != 0; --i) {
    bbs_step(bbs); r = (r << 1) | (bbs->x & 1);
  }
  return r;
}
static uint64_t bbs_next64(bbs_t * bbs) {
  uint64_t r = 0;
  for (int i = 64; i != 0; --i) {
    bbs_step(bbs); r = (r << 1) | (bbs->x & 1);
  }
  return r;
}

A parallel version of the generator can be implemented to slightly alleviate its slowness:

static void bbs_nextbytes(bbs_t * bbs, void * bp, size_t len) {
  uint8_t * buf = bp;
#ifndef OPENMP
  for (size_t i = 0; i < len; i++) {
    uint8_t r = 0;
    for (int i = 8; i != 0; --i) {
      bbs_step(bbs); r = (r << 1) | (bbs->x & 1);
    }
    buf[i] = r;
  }
#else
  size_t threads;
  #pragma omp parallel
  {
    #pragma omp single
    threads = omp_get_num_threads();
  }
  size_t chunk = len / threads;
  #pragma omp parallel for schedule(static)
  for (size_t i = 0; i < threads; i++) {
    bbs_t clone = *bbs;
    bbs_set(&clone, bbs->pos + i * chunk * 8);
    for (size_t j = 0; j < chunk; j++) {
      uint8_t r = 0;
      for (int i = 8; i != 0; --i) {
        bbs_step(&clone); r = (r << 1) | (clone.x & 1);
      }
      buf[i * chunk + j] = r;
    }
  }
  bbs_set(bbs, bbs->pos + len * 8);
  size_t remainder = len % threads;
  for (size_t i = 0; i < remainder; i++) {
    uint8_t r = 0;
    for (int i = 8; i != 0; --i) {
      bbs_step(bbs); r = (r << 1) | (bbs->x & 1);
    }
    buf[len - remainder + i] = r;
  }
#endif
}

Via the CLI stub we can both do some rudimentary checks and generate some pseudo-random numbers. Alternatively, we can also test the output so that it can be fed into a statistical test suite such as the NIST SP 800-22 or Diehard tests:

// ---------------------------------------------------------------------------
//      CLI stub. By default, the program will output
//      an infinite stream of random numbers to stdout (64-bit,
//      native endian). If changed, it displays an experiment.
// ---------------------------------------------------------------------------
#if 0
int main(void) {
  init_secrandom();  populate_barrett_cache();
  bbs_t bbs;  bbs_new(&bbs);
  uint8_t * buffer = malloc(1 << 24);
  for (;;) {
    bbs_nextbytes(&bbs, buffer, 1 << 24);
    fwrite(buffer, 1, 1 << 24, stdout);
  }
}
#else
int main(void) {
  init_secrandom();  populate_barrett_cache();
  bbs_t bbs;  bbs_new(&bbs);
  uint8_t buf[64];
  printf("Current position: %d\n", bbs.pos);
  printf("Probing 64 bytes of data: ");
  bbs_nextbytes(&bbs, buf, 64);
  for (int i = 0; i < 64; i++)
    printf("%02x", buf[i]);
  printf("\n");
  printf("Current position: %d\n", bbs.pos);
  printf("Probing another 64 bytes of data: ");
  bbs_nextbytes(&bbs, buf, 64);
  for (int i = 0; i < 64; i++)
    printf("%02x", buf[i]);
  printf("\n");
  printf("Rewinding to position 512.\n");
  bbs_set(&bbs, 512);
  printf("Current position: %d\n", bbs.pos);
  printf("Probing 64 bytes of data: ");
  bbs_nextbytes(&bbs, buf, 64);
  for (int i = 0; i < 64; i++)
    printf("%02x", buf[i]);
  printf("\n");
}
#endif

Miscellaneous results.⌗

The period of the BBS generator is strictly tied to the Carmichael function. BBS is ultimately periodic with period $\lambda(\lambda(n))$ . Hence minimising $\gcd((p-3)/2, (q-3)/2)$ is crucial for security, as it maximises $\lambda(n)$ , which in turn tends to maximise $\lambda(\lambda(n))$ .
The existence of one-way functions is equivalent to the existence of pseudorandom generators that pass all polynomial-time statistical tests. The proof of this is given by J. Hastad, R. Impagliazzo, L. Levin, and M. Luby. A Pseudorandom Generator from any One-way Function in SIAM J. Computing, 28(4):1364-1396, April 1999.
The so-called proof of security is rather misleading - its practical consequences are not as significant as it may seem. Most importantly, dated literature about BBS tends to underestimate the magnitude of the parameters to the generator. The magnitude of 6800 bits in the modulus results in extremely slow generation of pseudo-random numbers.
The generator is very slow. For $n=512$ in parallel mode, we generate only about 2.65MB/s of random data. $n=1024$ yields a more depressing figure of 721.6kB/s. Predictably, the functions __divmodbitint4 and __mulbitint3 constitute the majority of the runtime (>95%) with an equal proportion between them. Future improvements could involve the use of the Chinese Remainder Theorem for faster computation. Operation in the Montgomery domain could also be evaluated. The author hopes that future releases of GCC ship a __mulbitint3 function that is not quadratic but perhaps uses Karatsuba or such.
An simple implementation using GMP (and thus is not constant-time, and is more vulnerable to side-channel attacks) put together by the author at hand can accomplish the rate of about 3.1MB/s for $n=1024$ . The author is interested in investigating this as a future project and specialising the parts of the GMP responsible for the speedup for the BBS generator.

A Survey of Results on the Blum-Blum-Shub Pseudorandom Number Generator