SK(I) calculus reduction in asm2bf - Part 1
Background⌗
Back in January of 2021, I entered a small duel - the person to make the smallest SK calculus reduction machine in brainfuck before the deadline wins. As the author of asm2bf, I feel fairly confident working with it, so I thought that I could write a simple SK calculus reductor, and then optimise it for size using various tricks up my sleeve.
Let’s dive into the code⌗
The original source code for the SK calculus evaluator is now listed as an asm2bf example, so you can browse it in the asm2bf repository. In this blog post, I’ll try to just dissect it.
; SK calculus evaluator.
; Doesn't garbage collect, has very limited recursion depth.
; you can tweak this limit by changing the `stk` parameter below.
; Copyright (C) Kamila Szewczyk, 2021.
[bits 8]
stk 38
org 0
&heap
db 2
&changed
db 0
The beginning of the code is fairly self-explanatory. We’re limited to 8-bit brainfuck, so we make sure that asm2bf guards us against overflowing something known at the compile-time. Because the evaluator is recursive, it requires some stack space. The “default” version ships with 38 cells of stack space. We assume that the heap starts from the second cell of memory, and we declare a special global variable changed which faciliates putting the single-combinator reducing function in a fixpoint.
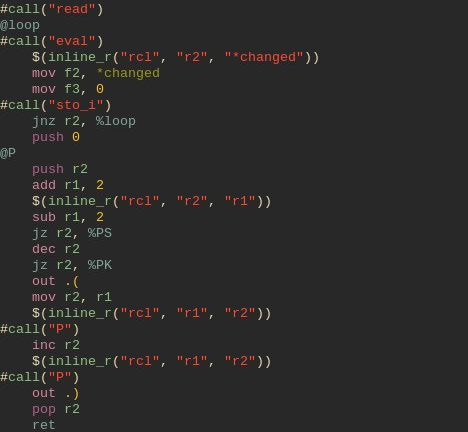
#call("read")
@loop
#call("eval")
rcl r2, *changed
vxcall sto *changed, 0
jnz r2, %loop
To start things off - main program loop. We read the SK calculus term, then reduce it, reset the changed variable and stop the reduction process if the term wasn’t changed. Next up - a fairly smart optimisation and a recursive term printing function:
push 0
@P
push r2
add r1, 2
rcl r2, r1
sub r1, 2
jz r2, %PS
dec r2
jz r2, %PK
out .(
mov r2, r1
rcl r1, r2
#call("P")
inc r2
rcl r1, r2
#call("P")
out .)
pop r2
ret
@PS
out .S
pop r2
ret
@PK
out .K
pop r2
ret
P is a function. We don’t call it, since by the end of evaluation we have to print the resulting term and labels in asm2bf exhibit the fallthru behavior. The problem here is that the P function returns to the label which is expected to be pushed on the stack. As an optimisation, I decided to push 0 and let the procedure code execute, so that when it’s done, it jumps to the label with ID 0, which terminates the program.
Then, we have a simple bump allocator that allocates 3 cells of memory at a time and tags the allocated memory area with the value in r1:
@A
rcl f3, *heap
add f3, 2
sto f3, r1
inc f3
ots f3, *heap
sub f3, 3
mov r1, f3
ret
In other words, @A allocates a single tree node which is used to represent the SKI calculus expression.
Next up, we have something that resembles the print function from earlier, except @read allocates and reads a single SK calculus term. The RS and RK cases take care of, respectively, the S and K calculus, while the later part takes care of binary tree nodes. From this function, it is easy to infer that the node structure in memory is [type] [node 1] [node 2], where [type] is either 0 (S), 1 (K) or 2 (binary tree node).
@read
push r2
in r2
ceq r2, .S
cjnz %RS
ceq r2, .K
cjnz %RK
mov r1, 2
#call("A")
mov r2, r1
#call("read")
sto r2, r1
#call("read")
inc r2
sto r2, r1
dec r2
mov r1, r2
in r2
pop r2
ret
@RS
mov r1, 0
#call("A")
pop r2
ret
@RK
mov r1, 1
#call("A")
pop r2
ret
Now, everything left is the evaluation function:
@eval
push r2
push r3
rcl r2, r1
jz r2, %skip
rcl r3, r2
jz r3, %skip
add r3, 2
rcl r4, r3
cne r4, 1
cjnz %skip
inc r2
rcl r3, r2
mov r1, r3
vxcall sto *changed, 1
jmp %not_bi
The first case we handle is the K combinator - first we check if the tree structure is correct, then we check if the combinator is K, and finally, we return the first argument to it.
The somewhat more involved case is the S combinator - it requires allocating a few new nodes, and in general involves weird node shuffling action. We start with checking if the tree is suitable to perform the S combinator reduction:
@skip
rcl r2, r1
jz r2, %notS
rcl r3, r2
jz r3, %notS
rcl r4, r3
jz r4, %notS
add r4, 2
rcl r2, r4
jnz r2, %notS
Then according to the (((Sx)y)z) => ((xz)(yz)) rule, we transform the tree allocating two new nodes for (xz) and (yz), and the final node to contain these two. Everything is doable within just registers.
inc r1
rcl r6, r1
dec r1
rcl r2, r1
rcl r3, r2
inc r2
inc r3
rcl r5, r2
rcl r4, r3
mov r1, 2
#call("A")
mov r2, r1
mov r1, 2
#call("A")
sto r2, r1
sto r1, r4
inc r1
sto r1, r6
mov r1, 2
#call("A")
inc r2
sto r2, r1
dec r2
sto r1, r5
inc r1
sto r1, r6
mov r1, r2
vxcall sto *changed, 1
jmp %not_bi
Last but not least, we have to account for the case where we have to go deeper to reduce an expression, so we finish the reduction function with a double recursion on both binary tree nodes:
@notS
rcl r2, r1
cge r2, 2
cjz %not_bi
mov r3, r1
rcl r1, r3
#call("eval")
sto r3, r1
inc r3
rcl r1, r3
#call("eval")
sto r3, r1
dec r3
mov r1, r3
And at the end of our reduction procedure we embed a common return point which pops off the preserved registers and returns.
@not_bi
pop r3
pop r2
ret
The code golf part - making asm2bf shine⌗
There are two obvious problems with this code. First, the stack takes a lot of space, so sto, rcl & friends will emit many >s an <s to get to the taperam. Second, the registers are picked suboptimally (because the code was written by a human). Third, too much stuff is preserved and move semantics weren’t utilised at all. The generated brainfuck code is 36 kilobytes big - not bad, but not great either.
We start off with fixing the first problem by creating stub functions for sto and rcl. While at it, we also add the move ^ prefix to a few instructions where preserving isn’t required.
; SK calculus evaluator.
; Doesn't garbage collect, has very limited recursion depth.
; you can tweak this limit by changing the `stk` parameter below.
; Copyright (C) Kamila Szewczyk, 2021.
[bits 8]
stk 38
org 0
&heap
db 2
&changed
$(
function def_inline(ins)
print("@" .. ins .. "_i\n" .. ins .. " f2, f3\nret\n")
end
function inline(ins, arg1, arg2)
print("mov f2, " .. arg1 .. "\nmov f3, " .. arg2 .. "\n")
call(ins .. "_i")
end
function inline_r(ins, arg1, arg2)
print("mov f3, " .. arg2 .. "\n")
call(ins .. "_i")
print("mov " .. arg1 .. ", f2")
end
)
#call("read")
@loop
#call("eval")
$(inline_r("rcl", "r2", "*changed"))
mov f2, *changed
mov f3, 0
#call("sto_i")
^jnz r2, %loop
^push 0
@P
^push r2
add r1, 2
$(inline_r("rcl", "r2", "r1"))
sub r1, 2
jz r2, %PS
dec r2
jz r2, %PK
out .(
^mov r2, r1
$(inline_r("rcl", "r1", "r2"))
#call("P")
inc r2
$(inline_r("rcl", "r1", "r2"))
#call("P")
out .)
pop r2
ret
@PS
out .S
pop r2
ret
@PK
out .K
pop r2
ret
@A
mov f3, *heap
#call("rcl_i")
add f2, 2
^mov f3, r1
#call("sto_i")
inc f2
ots f2, *heap
sub f2, 3
^mov r1, f2
ret
@read
^push r2
in r2
ceq r2, .S
cjnz %RS
ceq r2, .K
cjnz %RK
mov r1, 2
#call("A")
mov r2, r1
#call("read")
$(inline("sto", "r2", "r1"))
#call("read")
inc r2
$(inline("sto", "r2", "r1"))
dec r2
^mov r1, r2
in r2
pop r2
ret
@RS
mov r1, 0
#call("A")
pop r2
ret
@RK
mov r1, 1
#call("A")
pop r2
ret
@eval
^push r2
^push r3
$(inline_r("rcl", "r2", "r1"))
jz r2, %skip
$(inline_r("rcl", "r3", "r2"))
jz r3, %skip
add r3, 2
$(inline_r("rcl", "r4", "r3"))
cne r4, 1
cjnz %skip
inc r2
$(inline_r("rcl", "r3", "r2"))
mov r1, r3
mov f2, *changed
mov f3, 1
#call("sto_i")
jmp %not_bi
@skip
$(inline_r("rcl", "r2", "r1"))
jz r2, %notS
$(inline_r("rcl", "r3", "r2"))
jz r3, %notS
$(inline_r("rcl", "r4", "r3"))
jz r4, %notS
add r4, 2
$(inline_r("rcl", "r2", "r4"))
jnz r2, %notS
inc r1
$(inline_r("rcl", "r6", "r1"))
dec r1
$(inline_r("rcl", "r2", "r1"))
$(inline_r("rcl", "r3", "r2"))
inc r2
inc r3
$(inline_r("rcl", "r5", "r2"))
$(inline_r("rcl", "r4", "r3"))
mov r1, 2
#call("A")
^mov r2, r1
mov r1, 2
#call("A")
$(inline("sto", "r2", "r1"))
$(inline("sto", "r1", "r4"))
inc r1
$(inline("sto", "r1", "r6"))
mov r1, 2
#call("A")
inc r2
$(inline("sto", "r2", "r1"))
dec r2
$(inline("sto", "r1", "r5"))
inc r1
$(inline("sto", "r1", "r6"))
mov r1, r2
mov f2, *changed
mov f3, 1
#call("sto_i")
jmp %not_bi
@notS
$(inline_r("rcl", "r2", "r1"))
cge r2, 2
cjz %not_bi
^mov r3, r1
$(inline_r("rcl", "r1", "r3"))
#call("eval")
$(inline("sto", "r3", "r1"))
inc r3
$(inline_r("rcl", "r1", "r3"))
#call("eval")
$(inline("sto", "r3", "r1"))
dec r3
^mov r1, r3
@not_bi
pop r3
pop r2
ret
#def_inline("sto")
#def_inline("rcl")
The size certainly improved - from 36 KB, we drop down to 30.2 KB, although this result still isn’t satisfactory for me. For this reason, I decided to replace all registers with fictional names and define them at the top of my source unit:
I’ve also noticed that eval doesn’t have to preserve the BX register, which lets me get rid of a push/pop pair. Either way, this preparation was conducted because I want to create write a tiny register allocator for asm2bf, which will find the most optimal register layout for our program given these constraints.
I decided to start off with a bit of code that generates us the register mappings given a permutation of numbers from 1 to 8:
f←{
regs←'r1' 'r2' 'r3' 'r4' 'r5' 'r6' 'f2' 'f3'
maps←'AX' 'BX' 'CX' 'DX' 'EX' 'FX' 'GX' 'HX'
⍺,⍨'?'∘,¨maps,¨'='∘,¨regs[⍵]
}
Next up, I mounted a 64M ramdisk at /mnt/ramdisk and removed the ?...=... headers from my source code. Let’s write a function that will test a specific layout:
try←{
r←'r1' 'r2' 'r3' 'r4' 'r5' 'r6' 'f2' 'f3'
m←'AX' 'BX' 'CX' 'DX' 'EX' 'FX' 'GX' 'HX'
_←(⊂⍺,⍨'?'∘,¨m,¨'='∘,¨r[⍵])⎕NPUT'/mnt/ramdisk/X.asm' 1
_←⎕SH'bfmake /mnt/ramdisk/X.asm'
≢⊃⊃⎕NGET'/mnt/ramdisk/X.b' 1
}
I have inlined the f function, beause it seemed relatively convenient. I could have used ⎕NSIZE instead of ⎕NGET, but it doesn’t yield a significant performance improvement and complicates the code a little, because ⎕NSIZE expects a number tied with a file, not a file name. Either way, now it’s time to import the pmat function from dfns and write a stub function that tests the entire permutation matrix from 1 to 8:
run←{
str←⊃⎕NGET ⍵ 1
m←↓pmat 8
s←⍕≢m
⎕←∊'total: 's
m[(⊃⍋)((⍳≢m){
size←str try ⍵
0=500|⍺:{_←⎕←∊(⍕⍵)'/'s ⋄ size}⍺
size
}¨m)]
}
Finally, I ran the function on the input file and went to make myself a coffee and take a short break. When I came back, I was greeted with the following:
run '/home/palaiologos/Desktop/workspace/asmbf/examples/tiny_sk.asm'
total: 40320
500/40320
1000/40320
[...]
39500/40320
40000/40320
┌───────────────┐
│3 2 5 6 7 8 1 4│
└───────────────┘
Brilliant! Now we know what is the best permutation! It appears that the size of our program decreased by a few kilobytes:
str try 3 2 5 6 7 8 1 4
27469
The try function generated our new assembly listing in the ramdisk, so I snatched it from there:
?AX=r3
?BX=r2
?CX=r5
?DX=r6
?EX=f2
?FX=f3
?GX=r1
?HX=r4
Finally, after removing the redundant PUSH BX/POP BX part, the size of our program settles on 27312 bytes.
Benchmarks⌗
Each value is the run time in seconds for the following test suite:
| Interpreter | ||||||
| tritium | bfi | |||||
| Program | Minimum | Maximum | Average | Minimum | Maximum | Average |
| tiny-sk, registers | 0.218 | 0.238 | 0.221 | 7.702 | 7.896 | 7.801 |
| tiny-sk, plain | 0.229 | 0.255 | 0.241 | 7.614 | 7.799 | 7.646 |
| sk | 0.208 | 0.223 | 0.208 | 6.440 | 6.619 | 6.500 |
To no surprise, plain sk is faster than any tiny-sk, because of less indirection. Register-optimized version of tiny-sk seems to be faster on tritium, and a little slower on bfi, which was fairly unexpected.
BFVM’s say⌗
There’s a different way of approaching the problem. We could take sk (tiny_sk won’t work since it uses move semantics + it won’t be any faster because of the thunks it uses for sto/rcl) and compile it using BFVM and then clang to get a decent native binary.
The results oscillate around 0.027s and 0.082s, with 0.032s being the average value. We’ve beaten tritium!